 Un
pendule simple est formé d'une boule de masse m
suspendu par un fil supposé sans masse et de longueur l.
Un
pendule simple est formé d'une boule de masse m
suspendu par un fil supposé sans masse et de longueur l. Un
pendule simple est formé d'une boule de masse m
suspendu par un fil supposé sans masse et de longueur l.
Un
pendule simple est formé d'une boule de masse m
suspendu par un fil supposé sans masse et de longueur l.
Lorsqu'on écarte le pendule de sa position d'origine, le vecteur poids se décompose en une force ayant pour direction le fil et qui se trouve donc être opposée à la tension du fil et d'une force F normale au fil qui est responsable du mouvement de rappel.
De façon plus précise P = m g
et F = m g sin a = m
![]() où
où
![]() est l'accélération tangentielle de la masse m.
est l'accélération tangentielle de la masse m.
Comme l'accélération angulaire a"
vérifie
![]() on obtient :
on obtient :
(e) :
![]()
On ne sait pas résoudre directement cette équation mais si l'angle a est petit on peut remplacer sin a par a et (e) devient alors :
(e1) :
![]()
(e1) est une équation linéaire
que l'on sait résoudre; en effet son équation
caractéristique
![]()
a pour racines
![]() et (e1) a donc pour solutions :
et (e1) a donc pour solutions :![]() ,
a0 et
,
a0 et
![]() étant des constantes dépendantes de la position et de
la vitesse à l'instant initial.
étant des constantes dépendantes de la position et de
la vitesse à l'instant initial.
De plus si a est petit et si le pendule subit un amortissement proportionnel à la vitesse angulaire alors l'équation différentielle devient :
(e2) :
![]() où k est le
coefficient d'amortissement.
où k est le
coefficient d'amortissement.
(e2)
est une équation linéaire ; son équation
caractéristique est
![]() C'est une équation du second degré de discriminant
C'est une équation du second degré de discriminant
![]()
| Si L'équation différentielle a dans ce cas pour solution : 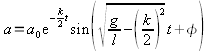 C'est ce qu'on appelle un régime pseudo-périodique. L'enveloppe de la courbe a pour équation |
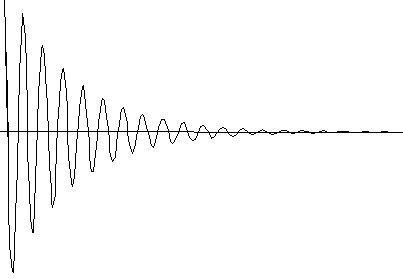 |
| Si |
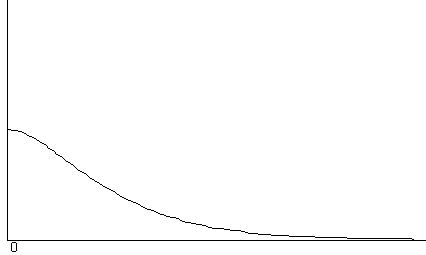 |
| Si |
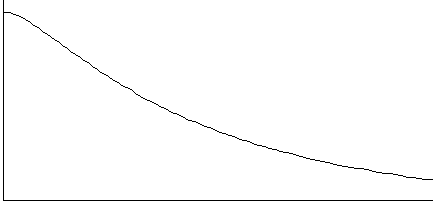 |